揭秘：圆周率小数点后第1000位数字竟然是……

圆周率π，作为数学中的一个基本常数，表示圆的周长与其直径之比，其值约为3.14159。然而，这个数值只是一个近似值，实际上圆周率是一个无理数，即它的小数部分是无限不循环的。正是这种无限不循环的特性，使得圆周率成为了数学和物理学等多个领域的研究热点。那么，圆周率小数点后1000位是几呢？

以下是圆周率小数点后1000位的完整数字序列：

3.14159 26535 89793 23846 26433 83279 50288 41971 69399 37510 58209 74944 59230 78164 06286 20899 86280 34825 34211 70679 82148 08651 32823 06647 09384 46095 50582 23172 53594 08128 48111 74502 84102 70193 85211 05559 64462 29489 54930 38196 44288 10975 66593 34461 28475 64823 37867 83165 27120 19091 45648 56692 34603 48610 45432 66482 13393 60726 02491 41273 72458 70066 06315 58817 48815 20920 96282 92540 91715 36436 78925 90360 01133 05305 48820 46652 13841 46951 94151 16094 33057 27036 57595 91953 09218 61173 81932 61179 31051 18548 07446 23799 62749 56735 18857 52724 89122 79381 83011 94912 98336 73362 44065 66430 86021 39494 63952 24737 19070 21798 60943 70277 05392 17176 29317 67523 84674 81846 76694 05132 00056 81271 45263 56082 77857 71342 75778 96091 73637 17872 14684 40901 22495 34301 46549 58537 10507 92279 68925 89235 42019 95611 21290 21960 86403 44181 59813 62977 47713 09960 51870 72113 49999 99837 29780 49951 05973 17328 16096 31859 50244 59455 34690 83026 42522 30825 33446 85035 26193 11881 71010 00313 78387 52886 58753 32083 81420 61717 76691 47303 59825 34904 28755 46873 11595 62863 88235 37875 93751 95778 18577 80532 17122 68066 13001 92787 66111 95909 21642 01989

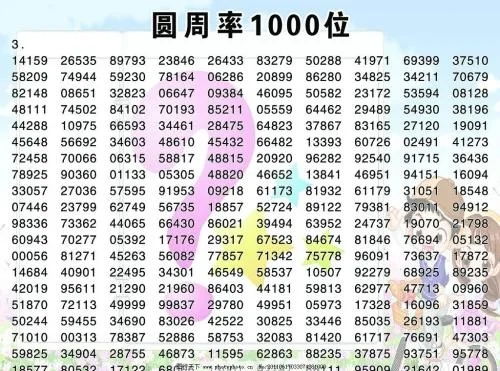
在上述序列中，圆周率小数点后第1000位的数字是9。

圆周率的这一特性使得它成为了众多数学家和物理学家研究的对象。在历史上，许多数学家都致力于计算圆周率的更精确值。随着计算机技术的发展，人们已经能够计算出圆周率小数点后数亿位，这为科学研究提供了极大的便利。

圆周率不仅在数学领域有着重要的应用，还在物理学、工程学等多个领域发挥着关键作用。例如，在物理学中，圆周率经常出现在与圆相关的物理现象和公式中，如波动方程、电磁场理论等。在工程学中，圆周率的精确值对于设计圆形结构、计算面积和周长等具有重要意义。

此外，圆周率还成为了数学和计算机科学中的一个挑战性问题。许多数学家和计算机科学家致力于开发更高效、更精确的算法来计算圆周率的值。这些算法不仅推动了数学和计算机科学的发展，还为我们更深入地理解圆周率这一神秘常数提供了有力的工具。

对于普通人来说，虽然圆周率的精确值在日常生活中可能并不常用，但了解圆周率的基本概念和性质仍然具有重要意义。它不仅可以帮助我们更好地理解数学和物理学中的一些基本概念和公式，还可以激发我们对科学的好奇心和探索欲。

总之，圆周率小数点后1000位是9，这一事实展示了圆周率的无限不循环特性。作为数学中的一个基本常数，圆周率在多个领域都有着广泛的应用和重要性。通过不断研究和探索圆周率的性质和应用，我们可以更深入地理解这个神秘而迷人的常数。